Interpolacja wielomianowa
Interpolacja wielomianowa, nazywana też interpolacją Lagrange'a, od nazwiska pioniera badań nad interpolacją Josepha Lagrange'a, lub po prostu interpolacją jest metodą numeryczną przybliżania funkcji tzw. wielomianem Lagrange'a stopnia n, przyjmującym w n+1 punktach, zwanych węzłami interpolacji wartości takie same jak przybliżana funkcja.
Interpolacja jest często stosowana w naukach doświadczalnych, gdzie dysponuje się zazwyczaj skończoną liczbą danych do określenia zależności między wielkościami.
Zgodnie z twierdzeniem Weierstrassa dowolną funkcję y=f(x) ciągłą na przedziale domkniętym można dowolnie przybliżyć za pomocą wielomianu odpowiednio wysokiego stopnia.
Znajdowanie odpowiedniego wielomianu
Wielomian przyjmujący zadane wartości w konkretnych punktach można zbudować w ten sposób:
- Dla pierwszego węzła o wartości
 znajduje się wielomian, który w tym punkcie przyjmuje wartość
znajduje się wielomian, który w tym punkcie przyjmuje wartość  , a w pozostałych węzłach
, a w pozostałych węzłach  wartość zero.
wartość zero. - Dla kolejnego węzła znajduje sie podobny wielomian, który w drugim węźle przyjmuje wartość
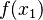 , a w pozostałych węzłach
, a w pozostałych węzłach  wartość zero.
wartość zero. - Dodaje się wartość ostatnio obliczonego wielomianu do wartości poprzedniego
- Dla każdego z pozostałych węzłów znajduje się podobny wielomian, za każdym razem dodając go do wielomianu wynikowego
- Wielomian będący sumą wielomianów obliczonych dla poszczególnych węzłów jest wielomianem interpolującym
Dowód ostatniego punktu i dokładny sposób tworzenia poszczególnych wielomianów opisany jest poniżej w dowodzie istnienia wielomianu interpolującego będącego podstawą algorytmu odnajdowania tego wielomianu.
Dowód istnienia wielomianu interpolującego
Niech  będą węzłami interpolacji funkcji
będą węzłami interpolacji funkcji 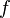 takimi, że znane są wartości
takimi, że znane są wartości 
Można zdefiniować funkcję:
 będą węzłami interpolacji funkcji
będą węzłami interpolacji funkcji 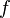 takimi, że znane są wartości
takimi, że znane są wartości 
Można zdefiniować funkcję:
 ,
, 
taką, że dla 
 jest wielomianem stopnia
jest wielomianem stopnia  (mianownik jest liczbą, a licznik iloczynem
(mianownik jest liczbą, a licznik iloczynem  wyrazów postaci
wyrazów postaci  )
)

 jest wielomianem stopnia
jest wielomianem stopnia  (mianownik jest liczbą, a licznik iloczynem
(mianownik jest liczbą, a licznik iloczynem  wyrazów postaci
wyrazów postaci  )
)- Gdy
 i
i  :
:
- Gdy
 i
i  :
:
(licznik = 0 ponieważ występuje element
 )
)Niech
 będzie wielomianem stopnia co najwyżej
będzie wielomianem stopnia co najwyżej  , określonym jako:
, określonym jako:Dla

 .
.
Wszystkie składniki sumy o indeksach różnych od
 są równe zeru (ponieważ dla
są równe zeru (ponieważ dla  , składnik o indeksie
, składnik o indeksie  jest równy:
jest równy: .
.
A więc
z czego wynika, że  jest wielomianem interpolującym funkcję
jest wielomianem interpolującym funkcję  w punktach
w punktach  .
.
 jest wielomianem interpolującym funkcję
jest wielomianem interpolującym funkcję  w punktach
w punktach  .
.Jednoznaczność interpolacji wielomianowej
Dowód
Załóżmy, że istnieją dwa tożsamościowo różne wielomiany  i
i  stopnia
stopnia  , przyjmujące w węzłach
, przyjmujące w węzłach  takie same wartości.
takie same wartości.
Niech
 i
i  stopnia
stopnia  , przyjmujące w węzłach
, przyjmujące w węzłach  takie same wartości.
takie same wartości.Niech
będzie wielomianem. Jest on stopnia co najwyżej
 (co wynika z własności odejmowania wielomianów).
(co wynika z własności odejmowania wielomianów).Ponieważ
 i
i  w węzłach
w węzłach  interpolują tę samą funkcję, to
interpolują tę samą funkcję, to  , a więc
, a więc  (węzły interpolacji są pierwiastkami
(węzły interpolacji są pierwiastkami  ).(*)
).(*)Ale każdy niezerowy wielomian stopnia
 ma co najwyżej
ma co najwyżej  pierwiastków rzeczywistych, a ponieważ z (*) wiadomo, że
pierwiastków rzeczywistych, a ponieważ z (*) wiadomo, że  ma
ma  pierwiastków, to
pierwiastków, to  musi być wielomian tożsamościowo równy zeru. A ponieważ
musi być wielomian tożsamościowo równy zeru. A ponieważ
to
co jest sprzeczne z założeniem, że
 i
i  są różne.
są różne.Błąd interpolacji
Dość naturalne wydaje się przyjęcie, że zwiększenie liczby węzłów interpolacji (lub stopnia wielomianu interpolacyjnego) pociąga za sobą coraz lepsze przybliżenie funkcji f(x) wielomianem  . Idealna byłaby zależność:
. Idealna byłaby zależność:
 . Idealna byłaby zależność:
. Idealna byłaby zależność: ,
,
tj. dla coraz większej liczby węzłów wielomian interpolacyjny staje się "coraz bardziej podobny" do interpolowanej funkcji.
Dla węzłów równo odległych tak być nie musi → efekt Rungego.
Można dowieść, że dla każdego wielomianu interpolacyjnego stopnia  , przybliżającego funkcję
, przybliżającego funkcję  w przedziale
w przedziale ![[a,b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) na podstawie
na podstawie  węzłów, istnieje taka liczba
węzłów, istnieje taka liczba  zależna od
zależna od  , że dla reszty interpolacji
, że dla reszty interpolacji 
 , przybliżającego funkcję
, przybliżającego funkcję  w przedziale
w przedziale ![[a,b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) na podstawie
na podstawie  węzłów, istnieje taka liczba
węzłów, istnieje taka liczba  zależna od
zależna od  , że dla reszty interpolacji
, że dla reszty interpolacji 
gdzie  , a
, a ![\xi \in [a;b]](http://upload.wikimedia.org/math/f/1/3/f1302a366e78b319c24f828cebac3bdc.png) jest liczbą zależną od x.
jest liczbą zależną od x.
 , a
, a ![\xi \in [a;b]](http://upload.wikimedia.org/math/f/1/3/f1302a366e78b319c24f828cebac3bdc.png) jest liczbą zależną od x.
jest liczbą zależną od x.
Do oszacowania z góry wartości  można posłużyć się wielomianami Czebyszewa stopnia
można posłużyć się wielomianami Czebyszewa stopnia  do oszacowania wartości
do oszacowania wartości  dla
dla ![x\in [-1,1]](http://upload.wikimedia.org/math/5/4/7/547db7d2339cfb3345123313fe6a4981.png) . Dla przedziału
. Dla przedziału ![[a,b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) wystarczy dokonać przeskalowania wielomianu
wystarczy dokonać przeskalowania wielomianu 
 można posłużyć się wielomianami Czebyszewa stopnia
można posłużyć się wielomianami Czebyszewa stopnia  do oszacowania wartości
do oszacowania wartości  dla
dla ![x\in [-1,1]](http://upload.wikimedia.org/math/5/4/7/547db7d2339cfb3345123313fe6a4981.png) . Dla przedziału
. Dla przedziału ![[a,b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) wystarczy dokonać przeskalowania wielomianu
wystarczy dokonać przeskalowania wielomianu 
Źródło : http://pl.wikipedia.org/wiki/Interpolacja_wielomianowa








Brak komentarzy:
Prześlij komentarz