Interpolacja
Wyróżniamy pięć rodzajów interpolacji :
Interpolacja (grafika komputerowa)
Interpolacja – w grafice komputerowej jest to proces mający na celu utworzenie nowego, wcześniej nieistniejącego piksela na podstawie pikseli sąsiadujących z pikselem tworzonym tak, aby był on jak najlepiej dopasowany optycznie do przetwarzanego obrazu. Interpolację wykorzystuje się przy resamplingu, uzupełnianiu i korygowaniu obrazów oraz automatycznej korekcie obrazów w skanerach do filmów.
Rodzaje
Istnieją cztery główne rodzaje interpolacji:
- Interpolacja metodą "najbliższego sąsiada", ang. nearest neighbor - przy powiększaniu odbywa się wierne kopiowanie najbliższego piksela. W przypadku skalowania innego niż o wielokrotność 100% jest to statystyczne kopiowanie niektórych pikseli. Przy pomniejszaniu jest to mechaniczne pomijanie niektórych pikseli. Metoda najprostsza i wymagająca od komputera najmniejszej mocy obliczeniowej. Jest to interpolacja rzadko stosowana, ponieważ w przypadku dużych powiększeń wyraźnie widać grupy identycznych pikseli, a granice pomiędzy pikselami są wyraźne, ostre, nie rozmyte. Metoda dobra przy obrabianiu zrzutów z ekranu monitora, np. okien dialogowych, przycisków. Można jej także użyć do najbardziej kontrastowych obrazów, oraz obrazów o motywach wyraźnie ułożonych na siatce. Decyzję należy podjąć drogą eksperymentu - wszystko zależy od oczekiwanych rezultatów. Jest to jedyna interpolacja nie powodująca rozmycia kształtów – owo rozmycie jest jednak najczęściej potrzebne dla zachowania naturalnego wyglądu obrazu.
- Interpolacja dwuliniowa, ang. bilinear - metoda pośrednia, trochę bardziej obciąża komputer ale i daje lepszy, łagodniejszy dla oczu obraz. Piksele są powielane lub redukowane z uwzględnieniem koloruczterech sąsiednich pikseli, stykających się z danym pikselem bokami.
- Interpolacja dwusześcienna, ang. bicubic – najlepszy efekt końcowy, opcja domyślna w większości programów. Krawędzie są naturalnie, łagodnie rozmyte, a obraz po transformacji najbardziej wśród tych trzech metod przypomina obraz początkowy. Metoda polega na uwzględnieniu kolorów wszystkich ośmiu pikseli stykających się bokami lub rogami z danym pikselem.
- Interpolacja algorytmem Lanczosa - uwzględniająca sąsiadujące punkty w kwadratach 4x4, 6x6 lub 8x8. W pierwszym przypadku algorytm jest zbliżony wynikami do interpolacji dwusześciennej, w pozostałych daje lepsze wyniki, ale czas wykonania obliczeń jest znacząco dłuższy.
Ponieważ obraz bitmapowy przypomina szachownicę lub papier milimetrowy, to wszelkie obracanie bitmapy o kąt inny niż wielokrotność 90 stopni odbywa się również na drodze interpolacji.
Interpolacja (kartografia)
Interpolacja (kartografia)
Interpolacja (matematyka)
Interpolacja – metoda numeryczna polegająca na wyznaczaniu w danym przedziale tzw. funkcji interpolacyjnej, która przyjmuje w nim z góry zadane wartości w ustalonych punktach, nazywanych węzłami. Stosowana jest ona często w naukach doświadczalnych, gdzie dysponuje się zazwyczaj skończoną liczbą danych do określenia zależności między wielkościami oraz w celu uproszczenia skomplikowanych funkcji, np. podczas całkowania numerycznego. Interpolacja jest szczególnym przypadkiem metod numerycznych typu aproksymacja.
Interpolacja wielomianowa
- Dla danych
 punktów pomiarowych istnieje jedyny wielomian stopnia co najwyżej n interpolujący te punkty.
punktów pomiarowych istnieje jedyny wielomian stopnia co najwyżej n interpolujący te punkty.
Zwykle zakłada się o funkcji interpolowanej, że jest ciągła, choć często dodaje się warunki różniczkowalności, które umożliwiają dokładniejsze oszacowania błędów przybliżeń. Najprostszym przypadkiem jest interpolacja liniowa, zadanie interpolacji dla dwóch węzłów  i
i  . Rozwiązaniem w klasie wielomianów pierwszego stopnia jest wtedy funkcja liniowa, której wykres przechodzi przez punkty
. Rozwiązaniem w klasie wielomianów pierwszego stopnia jest wtedy funkcja liniowa, której wykres przechodzi przez punkty 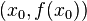 i
i 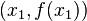 (por. rysunek).
(por. rysunek).
 i
i  . Rozwiązaniem w klasie wielomianów pierwszego stopnia jest wtedy funkcja liniowa, której wykres przechodzi przez punkty
. Rozwiązaniem w klasie wielomianów pierwszego stopnia jest wtedy funkcja liniowa, której wykres przechodzi przez punkty 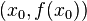 i
i 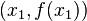 (por. rysunek).
(por. rysunek).Interpolacja (paleografia)
Interpolacja – w paleografii jest to wstawienie do istniejącego tekstu fragmentów (słów lub zdań), które oryginalnie się w tym tekście nie znajdowały. Może ona powstać w wyniku błędu kopisty lub drukarzaalbo być wynikiem kontaminacji.
Przykładem może posłużyć praktyka autorów Digestów 533 r. (część Kodyfikacji Justyniańskiej), którzy dostosowywali w ten sposób dzieła jurystów klasycznych do ówczesnych potrzeb.
Comma Johanneum może służyć jako przykład interpolacji.
Interpolacja (automatyka)
Rzeczywisty tor przemieszczania się końcówki robota często nie pokrywa się z torem określonym w programie. Tor, wzdłuż którego przemieszcza się końcówka robota, jest konsekwencją przemieszczania się każdego z napędów łańcucha kinematycznego, które jest zgodne z wektorem przemieszczenia, który z kolei jest wynikiem realizacji algorytmu sterującego według określonych wartości sterowniczych związanych z ruchem robota.
Fakt, iż tor rzeczywisty, po którym przemieszcza się końcówka robota, nie pokrywa się z torem określonym w programie, widać wyraźnie, gdy trajektoria zawarta w programie jest sumą kilku krzywych (np. interpolowanych naprzemiennie "po prostej" i "po okręgu"). Jest tak dlatego, że po każdym odcinku następuje bardzo krótkie zatrzymanie się robota w celu sprawdzenia położenia względem punktu docelowego. Po chwilowym zatrzymaniu się końcówki robota następuje natychmiastowe przemieszczenie się do następnego punktu. Dlatego też odwzorowanie toru zaprogramowanego nie jest płynne i nie pokrywa się dokładnie z torem zadanym.
Różnice są konsekwencją konieczności dokonywania ciągłych pomiarów jakości odwzorowywania drogi zadanej. Odchyłki te są odchyłkami dynamicznymi, ponieważ nie mogą przekraczać wartości dopuszczalnej, określonej dokładnością algorytmu sterowania (błąd odwzorowywania trajektorii).
Bloki programowe określające pozycje pośrednie (inaczej podporowe) manipulatora, gwarantujące zachowanie właściwego kształtu toru, nazywają się „interpolatorami trajektorii” (kształtują parametry zaprogramowanego kształtu trajektorii). Interpolator oblicza współrzędne punktów pośrednich  , trajektorii zgodnie z zadanym wzorcem drogi robota.
, trajektorii zgodnie z zadanym wzorcem drogi robota.
 , trajektorii zgodnie z zadanym wzorcem drogi robota.
, trajektorii zgodnie z zadanym wzorcem drogi robota.
Brak komentarzy:
Prześlij komentarz