czwartek, 29 listopada 2012
środa, 28 listopada 2012
poniedziałek, 19 listopada 2012
metody numeryczne- aproksymacja, METODY PROBALIBISTYCZNE PROCESY LOSOWE:
METODY PROBALIBISTYCZNE
PROCESY LOSOWE:
Pojęcie procesu losowego i jego opis
W punkcie II rozpatrywaliśmy zmienne losowe, które zależały tylko od przypadku czyli od  , w praktyce spotyka się na ogół bardziej skomplikowane wielkości losowe , które zmieniają się wraz ze zmianą pewnego parametru
, w praktyce spotyka się na ogół bardziej skomplikowane wielkości losowe , które zmieniają się wraz ze zmianą pewnego parametru  , są one zatem zależne zarówno od przypadku, jak i od wartości tego parametru. Inaczej mówiąc dla opisu wyniku doświadczenia nie wystarcza już punkt przestrzeni , a niezbędna jest funkcja wspomnianego parametru. Jednym z historycznie pierwszych przykładów takich wielkości jest każda współrzędna cząsteczki w tzw. ruchu Browna, która nie tylko jest zmienną losową, ale także zależy od czasu. Innym przykładem są szumy zniekształcające sygnały radiowe, które są zmiennymi losowymi (np. z powodu z wyładowań atmosferycznych), a także zależą od czasu. Także liczba zadań (procesów) w systemie komputerowym, czy liczba pojazdów przejeżdżające przez dane skrzyżowanie są zmiennymi losowymi zależnymi również od czasu. Podkreślmy, że parametrem od którego zależą wymienione (i inne wielkości losowe) zmienne losowe nie musi być czas np. w ruchu turbulentnym prędkość cząsteczki cieczy jest zmienną losową (trójwymiarową) zależną do punktu przestrzeni. W ogólności parametr, o którym mówimy nie musi mieć w ogóle żadnej interpretacji fizycznej. Rozszerzenie teorii prawdopodobieństwa pozwalające badać zmienne losowe zależne od danego parametru nazywa się teorią procesów losowych (przypadkowych,stochastycznych).
, są one zatem zależne zarówno od przypadku, jak i od wartości tego parametru. Inaczej mówiąc dla opisu wyniku doświadczenia nie wystarcza już punkt przestrzeni , a niezbędna jest funkcja wspomnianego parametru. Jednym z historycznie pierwszych przykładów takich wielkości jest każda współrzędna cząsteczki w tzw. ruchu Browna, która nie tylko jest zmienną losową, ale także zależy od czasu. Innym przykładem są szumy zniekształcające sygnały radiowe, które są zmiennymi losowymi (np. z powodu z wyładowań atmosferycznych), a także zależą od czasu. Także liczba zadań (procesów) w systemie komputerowym, czy liczba pojazdów przejeżdżające przez dane skrzyżowanie są zmiennymi losowymi zależnymi również od czasu. Podkreślmy, że parametrem od którego zależą wymienione (i inne wielkości losowe) zmienne losowe nie musi być czas np. w ruchu turbulentnym prędkość cząsteczki cieczy jest zmienną losową (trójwymiarową) zależną do punktu przestrzeni. W ogólności parametr, o którym mówimy nie musi mieć w ogóle żadnej interpretacji fizycznej. Rozszerzenie teorii prawdopodobieństwa pozwalające badać zmienne losowe zależne od danego parametru nazywa się teorią procesów losowych (przypadkowych,stochastycznych).
 , w praktyce spotyka się na ogół bardziej skomplikowane wielkości losowe , które zmieniają się wraz ze zmianą pewnego parametru
, w praktyce spotyka się na ogół bardziej skomplikowane wielkości losowe , które zmieniają się wraz ze zmianą pewnego parametru  , są one zatem zależne zarówno od przypadku, jak i od wartości tego parametru. Inaczej mówiąc dla opisu wyniku doświadczenia nie wystarcza już punkt przestrzeni , a niezbędna jest funkcja wspomnianego parametru. Jednym z historycznie pierwszych przykładów takich wielkości jest każda współrzędna cząsteczki w tzw. ruchu Browna, która nie tylko jest zmienną losową, ale także zależy od czasu. Innym przykładem są szumy zniekształcające sygnały radiowe, które są zmiennymi losowymi (np. z powodu z wyładowań atmosferycznych), a także zależą od czasu. Także liczba zadań (procesów) w systemie komputerowym, czy liczba pojazdów przejeżdżające przez dane skrzyżowanie są zmiennymi losowymi zależnymi również od czasu. Podkreślmy, że parametrem od którego zależą wymienione (i inne wielkości losowe) zmienne losowe nie musi być czas np. w ruchu turbulentnym prędkość cząsteczki cieczy jest zmienną losową (trójwymiarową) zależną do punktu przestrzeni. W ogólności parametr, o którym mówimy nie musi mieć w ogóle żadnej interpretacji fizycznej. Rozszerzenie teorii prawdopodobieństwa pozwalające badać zmienne losowe zależne od danego parametru nazywa się teorią procesów losowych (przypadkowych,stochastycznych).
, są one zatem zależne zarówno od przypadku, jak i od wartości tego parametru. Inaczej mówiąc dla opisu wyniku doświadczenia nie wystarcza już punkt przestrzeni , a niezbędna jest funkcja wspomnianego parametru. Jednym z historycznie pierwszych przykładów takich wielkości jest każda współrzędna cząsteczki w tzw. ruchu Browna, która nie tylko jest zmienną losową, ale także zależy od czasu. Innym przykładem są szumy zniekształcające sygnały radiowe, które są zmiennymi losowymi (np. z powodu z wyładowań atmosferycznych), a także zależą od czasu. Także liczba zadań (procesów) w systemie komputerowym, czy liczba pojazdów przejeżdżające przez dane skrzyżowanie są zmiennymi losowymi zależnymi również od czasu. Podkreślmy, że parametrem od którego zależą wymienione (i inne wielkości losowe) zmienne losowe nie musi być czas np. w ruchu turbulentnym prędkość cząsteczki cieczy jest zmienną losową (trójwymiarową) zależną do punktu przestrzeni. W ogólności parametr, o którym mówimy nie musi mieć w ogóle żadnej interpretacji fizycznej. Rozszerzenie teorii prawdopodobieństwa pozwalające badać zmienne losowe zależne od danego parametru nazywa się teorią procesów losowych (przypadkowych,stochastycznych).- Definicja 1
- Procesem losowym nazywamy rodzinę zmiennych losowych

zależnych od parametru t i określonych na danej przestrzeni probabilistycznej (Ω,A,P).
Innymi słowy proces losowy to losowa funkcja parametru t, czyli taka funkcja, która  jest zmienną losowa.
jest zmienną losowa.
 jest zmienną losowa.
jest zmienną losowa.
Zmienną losową Xt, którą proces losowy jest w ustalonej chwili  nazywamy wartością tego procesu.
nazywamy wartością tego procesu.
 nazywamy wartością tego procesu.
nazywamy wartością tego procesu.
Zbiór wartości wszystkich zmiennych losowych  , nazywamy przestrzenią stanu procesu losowego lub przestrzenią stanu.
, nazywamy przestrzenią stanu procesu losowego lub przestrzenią stanu.
 , nazywamy przestrzenią stanu procesu losowego lub przestrzenią stanu.
, nazywamy przestrzenią stanu procesu losowego lub przestrzenią stanu.
Jeśli zbiór jest skończony lub przeliczalny, to mówimy o procesach losowych z czasem dyskretnym. W pierwszym wypadku mamy do czynienia z n-wymiarową zmienną losową, a w drugim z odpowiednim ciągiem zmiennych losowych.
Choć niektóre klasy procesów losowych z czasem dyskretnym (np. łańcuchy Markowa) zasługują na uwagę, to jednak w dalszym ciagu skoncentrujemy się na procesach losowych z czasem ciągłym czyli takich, dla których T jest nieprzeliczalne.
Dla głębszego zrozumienia natury procesu losowego spójrzmy nań jeszcze z innej strony. Jak pamiętamy zmienna losowa przyporządkowywała zdarzeniu losowemu punkt w przestrzeni Rn. W przypadku procesu losowego mamy do czynienia z sytuacją gdy do opisu wyniku doświadczenia niezbędna jest funkcja ciągła, zwana realizacją procesu losowego.
W dalszym ciągu zakładamy, że mamy do czynienia ze skończonymi funkcjami losowymi, a zbiór wszystkich takich funkcji (realizacji) będziemy nazywali przestrzenią realizacji procesu losowego. Prowadzi to do drugiej definicji:
W dalszym ciągu zakładamy, że mamy do czynienia ze skończonymi funkcjami losowymi, a zbiór wszystkich takich funkcji (realizacji) będziemy nazywali przestrzenią realizacji procesu losowego. Prowadzi to do drugiej definicji:
- Definicja 2
- Procesem losowym nazywamy mierzalną względem P transformację przestrzeni zdarzeń elementarnych Ω w przestrzeni realizacji, przy czym realizacją procesu losowego nazywamy każdą skończoną funkcją rzeczywistą zmiennej
 .
.
Definicja powyższa wynika ze spojrzenia na proces losowy jako na funkcję dwóch zmiennych  i
i  , ustalając t otrzymujemy zmienną losową , a ustalając ω otrzymujemy realizację .
, ustalając t otrzymujemy zmienną losową , a ustalając ω otrzymujemy realizację .
 i
i  , ustalając t otrzymujemy zmienną losową , a ustalając ω otrzymujemy realizację .
, ustalając t otrzymujemy zmienną losową , a ustalając ω otrzymujemy realizację .
Na ogół na przestrzeń realizacji procesu losowego narzuca się pewne ograniczenia np. żeby to była przestrzeń Banacha (niezerowa i zwyczajna).
Reasumując: graficznie można przedstawić te dwa punkty widzenia w następujacy sposób.
Pełne oznaczenie procesu losowego ma zatem postać
 , lub
, lub 
przy czym w obu wypadkach zakłada się, że jest określona przestrzeń probabilistyczna .
.
 , lub
, lub 
przy czym w obu wypadkach zakłada się, że jest określona przestrzeń probabilistyczna
 .
.
Ponieważ jednak zależność od ω jako naturalną zwykle się pomija, otrzymujemy:
 , lub
, lub  .
.
 , lub
, lub  .
.
Ponadto, jeśli zbiór T jest zdefiniowany na początku rozważań to pomija się także zapis  i w rezultacie otrzymujemy :
i w rezultacie otrzymujemy :
Xt, lub X(t).
 i w rezultacie otrzymujemy :
i w rezultacie otrzymujemy :Xt, lub X(t).
Oznaczenie X(t) może zatem dotyczyć całego procesu losowego, jego jednej realizacji (dla ustalonego ω) lub jego jednej wartości, czyli zmiennej losowej (dla ustalonego t). Z kontekstu jednoznacznie wynika, o co w danym zapisie chodzi.
Przejdźmy do zapisu procesu losowego X(t). Będziemy rozpatrywać wyłącznie procesy losowe rzeczywiste (proces losowy zespolony ma postać: X(t) = X1(t) + iX2(t), gdzie X1(t) i X2(t) są procesami losowymi rzeczywistymi).
Ponieważ  proces losowy Xt jest zmienną, więc jego pełny opis w chwili t stanowi pełny rozkład prawdopodobieństwa tej zmiennej losowej. Rozkład taki nazywamy jednowymiarowym rozkładem prawdopodobieństwa procesu losowego. Jest on scharakteryzowany przez jednowymiarową dystrybuantę procesu losowego, w postaci :
proces losowy Xt jest zmienną, więc jego pełny opis w chwili t stanowi pełny rozkład prawdopodobieństwa tej zmiennej losowej. Rozkład taki nazywamy jednowymiarowym rozkładem prawdopodobieństwa procesu losowego. Jest on scharakteryzowany przez jednowymiarową dystrybuantę procesu losowego, w postaci :
F(x,t) = P[X(t) < x]
 proces losowy Xt jest zmienną, więc jego pełny opis w chwili t stanowi pełny rozkład prawdopodobieństwa tej zmiennej losowej. Rozkład taki nazywamy jednowymiarowym rozkładem prawdopodobieństwa procesu losowego. Jest on scharakteryzowany przez jednowymiarową dystrybuantę procesu losowego, w postaci :
proces losowy Xt jest zmienną, więc jego pełny opis w chwili t stanowi pełny rozkład prawdopodobieństwa tej zmiennej losowej. Rozkład taki nazywamy jednowymiarowym rozkładem prawdopodobieństwa procesu losowego. Jest on scharakteryzowany przez jednowymiarową dystrybuantę procesu losowego, w postaci :F(x,t) = P[X(t) < x]
Oczywiście rozkład jednowymiarowy procesu losowego nie charakteryzuje wzajemnej zależności między wartościami procesu (zmiennymi losowymi) w różnych chwilach. Jest on zatem ogólny tylko wtedy gdy dla dowolnych układow  wartości procesu losowego,są ciągami zmiennych losowych niezależnych, co na ogół nie zachodzi. W ogólności musimy zatem rozpatrywać łączny rozkład wartości procesu w różnych chwilach.
wartości procesu losowego,są ciągami zmiennych losowych niezależnych, co na ogół nie zachodzi. W ogólności musimy zatem rozpatrywać łączny rozkład wartości procesu w różnych chwilach.
 wartości procesu losowego,są ciągami zmiennych losowych niezależnych, co na ogół nie zachodzi. W ogólności musimy zatem rozpatrywać łączny rozkład wartości procesu w różnych chwilach.
wartości procesu losowego,są ciągami zmiennych losowych niezależnych, co na ogół nie zachodzi. W ogólności musimy zatem rozpatrywać łączny rozkład wartości procesu w różnych chwilach.- Definicja
- n-wymiarowym rozkładem prawdopodobieństwa procesu losowego nazywamy łączny rozkład prawdopodobieństwa i jego wartości dla dowolnego układu chwili t1,t2,...,tn , czyli łączny rozkład prawdopodobieństwa wektora losowego [X(t1),X(t2),...,X(tn)] opisany n - wymiarową dystrybuantą procesu losowego :
F(x1,t1;x2,t2;...;xn,tn) = P(X(t1) < x1,X(t2) < x2,...,X(tn) < xn) Momenty procesu losowego
Podobnie jak dla zmiennych losowych również dla procesów losowych definiuje się pewne proste charakterystyki rozkładu, w szczególności momenty. Mając jednowymiarowy rozkład procesu możemy określić jego jednowymiarowe momenty np. zdefiniowane poniżej.- Definicja
- Wartością średnią procesu losowego X(t) nazywamy funkcję m(t), która
 jest wartością średnią zmiennej losowej X(t), którą jest proces w chwili t:
jest wartością średnią zmiennej losowej X(t), którą jest proces w chwili t:
m(t) = E[X(t)]
- Definicja
- Wariancją procesu losowego X(t) nazywamy funkcję σ2(t), która
 jest wariancją zmiennej losowej X(t), którą jest proces w chwili t:
jest wariancją zmiennej losowej X(t), którą jest proces w chwili t:
σ2(t) = D2[X(t)] = E[X(t) − m(t)]2
Oczywiście jednowymiarowe momenty procesu losowego nie charakteryzują jego zależności pomiędzy wartościami procesu w różnych chwilach. Żeby opisywać te zależności musimy rozpatrywać wyższe momenty, w szczególności rozpatrzymy 2 różne chwile t1,t2 .- Definicja
- Funkcję korelacyjną procesu losowego X(t) definiujemy jako:
Rx(t1,t2) = E{[X(t1) − m(t1)][X(t2) − m(t2)]}
Procesy stacjonarne
Ponieważ ogólna teoria procesów losowych jest dla celów praktycznych zbyt skomplikowana rozpatruje się pewne klasy tych procesów spełniających dodatkowe założenia i upraszczające analizę. W dalszych punktach rozpatrzmy kilka takich klas zaczynając od procesów stacjonarnych. Rozpatruje się procesy stacjonarne w sensie węższym i szerszym.- Definicja
- Proces losowy X(t) nazywamy stacjonarnym w węższym sensie, jeśli dla dowolnego
 , dla dowolnego układu chwil t1,t2,...,tn dla dowolnego h takiego, że
, dla dowolnego układu chwil t1,t2,...,tn dla dowolnego h takiego, że 
 zachodzi:
zachodzi:
F(x1,t1;x2,t2;...;xn,tn) = F(x1,t1 + h;x2,t2 + h;...;xn,tn + h)
W szczególności dla n = 1 mamy:
F(x,t) = F(x,t + h)
co oznacza, że F(x,t) = F(x), zatem jednowymiarowe momenty takiego procesu nie zależą od t, w szczególności m(t) = m = const.Dla n = 2 mamy:
F(x1,t1;x2,t2) = F(x1,t1 + h;x2,t2 + h)
czyli
F(x1,t1;x2,t2) = F(x1,x2,τ)
gdzie τ = t2 − t1.Procesy o przyrostach niezależnych i procesy Markowa
- Definicja
- Proces losowy X(t) nazywamy procesem o przyrostach niezależnych jeżeli dla dowolnego ukladu
 (uporządkowany układ chwil) zmienne losowe
(uporządkowany układ chwil) zmienne losowe  są niezależne.
są niezależne.
Ważną klasą procesów niezależnych stanowią procesy Poissona.- Definicja
- Proces losowy X(t) nazywamy procesem Markowa jeśli dla każdego
 oraz dla dowolnych liczb rzeczywistych
oraz dla dowolnych liczb rzeczywistych  zachodzi
zachodzi![P[X(t_n) < x_n | X(t_{n-1}) = x_{n-1},X(t_{n-2}) = x_{n-2}, \cdots , X(t_1) = x_1] = P[X(t_n) < x_n | X(t_{n-1}) = x_{n-1}]](http://putwiki.informatyka.org/images/math/5/d/9/5d95835d3b16f3c29d7a2386bdc8a8ee.png)
- wielomianu (tzw. aproksymacja wielomianowa),
- funkcji sklejanych,
- funkcji matematycznych uzyskanych na drodze statystyki matematycznej (przede wszystkim regresji),
- sztucznych sieci neuronowych.
Ergodyczność procesów losowych
Zauważmy, że w celu wyznaczenia momentu procesu losowego musielibyśmy dysponować jednocześnie wszystkimi jego realizacjami, co w praktyce jest na ogół niemożliwe. W naturalny sposób powstaje więc pytanie, przy jakich założeniach można na podstawie pojedynczej realizacji procesu wyznaczyć jego momenty.
Odpowiedź na to pytanie jest przedmiotem tzw. twierdzeń ergodycznych, a procesy losowe dla których średnie po czasie (z pojedynczej realizacji) mogą być utożsamiane z odpowiednimi średnimi po zbiorze nazywają się procesami ergodycznymi względem odpowiedniego momentu (np. wartości średniej czy f. korelacyjnej).Można wykazać, że dla obszernej klasy procesów stacjonarnych warunek wystarczający ergodyczności względem wartości średniej i funkcji korelacyjnej ma postać: Zatem dla procesów stacjonarnych spełniajacych powyższy warunek mamy
Zatem dla procesów stacjonarnych spełniajacych powyższy warunek mamy![E[X(t)] = m \approx {1 \over T} \int_0^T X(t)dt](http://putwiki.informatyka.org/images/math/f/0/c/f0c097edb46008a64bfca1aa818fe7be.png) oraz
oraz![E \{ [X(t)-m][X(t+\tau)-m]\} = R_x(\tau) \approx {1 \over T} \int_0^T[X(t)-m][X(t+\tau)-m]dt](http://putwiki.informatyka.org/images/math/b/3/0/b3053d9ad9cf5965e206e08288328234.png) METODY NUMERYCZNEAPROKSYMACJAAproksymacja – proces określania rozwiązań przybliżonych na podstawie rozwiązań znanych, które są bliskie rozwiązaniom dokładnym w ściśle sprecyzowanym sensie. Zazwyczaj aproksymuje się byty (np. funkcje) skomplikowane bytami prostszymi.
METODY NUMERYCZNEAPROKSYMACJAAproksymacja – proces określania rozwiązań przybliżonych na podstawie rozwiązań znanych, które są bliskie rozwiązaniom dokładnym w ściśle sprecyzowanym sensie. Zazwyczaj aproksymuje się byty (np. funkcje) skomplikowane bytami prostszymi.Aproksymacja funkcji
Aproksymacje można wykorzystać w sytuacji, gdy nie istnieje funkcja analityczna pozwalająca na wyznaczenie wartości dla dowolnego z jej argumentów, a jednocześnie wartości tej nieznanej funkcji są dla pewnego zbioru jej argumentów znane. Mogą to być na przykład wyniki badań aktywności biologicznej dla wielu konfiguracji leków. Do wyznaczenia aproksymowanej aktywności biologicznej nieznanego leku można wówczas zastosować jedną z wielu metod aproksymacyjnych.
Aproksymowanie funkcji może polegać na przybliżaniu jej za pomocą kombinacji liniowej tzw. funkcji bazowych. Od funkcji aproksymującej, przybliżającej zadaną funkcję nie wymaga się, aby przechodziła ona przez jakieś konkretne punkty, tak jak to ma miejsce w interpolacji. Z matematycznego punktu widzenia aproksymacja funkcji w pewnej przestrzeni Hilberta
w pewnej przestrzeni Hilberta  jest zagadnieniem polegającym na odnalezieniu pewnej funkcji
jest zagadnieniem polegającym na odnalezieniu pewnej funkcji  gdzie
gdzie  jest podprzestrzenią
jest podprzestrzenią  tj.
tj.  takiej, by odległość (w sensie obowiązującej w
takiej, by odległość (w sensie obowiązującej w  normy) między
normy) między  a
a  była jak najmniejsza. Funkcja aproksymująca może wygładzać daną funkcję (gdy funkcja jest gładka, jest też różniczkowalna).Aproksymacja funkcji powoduje pojawienie się błędów, zwanych błędami aproksymacji. Dużą zaletą aproksymacji w stosunku do interpolacji jest to, że aby dobrze przybliżać, funkcja aproksymująca nie musi być wielomianem bardzo dużego stopnia (w ogóle nie musi być wielomianem). Przybliżenie w tym wypadku rozumiane jest jako minimalizacja pewnej funkcji błędu. Prawdopodobnie najpopularniejszą miarą tego błędu jest średni błąd kwadratowy, ale możliwe są również inne funkcje błędu, jak choćby błąd średni.Istnieje wiele metod aproksymacyjnych. Jednymi z najbardziej popularnych są: aproksymacja średniokwadratowa i aproksymacja jednostajna oraz aproksymacja liniowa, gdzie funkcją bazową jest funkcja liniowa.Wiele z metod aproksymacyjnych posiada fazę wstępną, zwaną również fazą uczenia oraz fazę pracy. W fazie wstępnej, metody te wykorzystując zadane pary punktów i odpowiadających im wartości aproksymacyjnych niejako „dostosowują” swoją strukturę wewnętrzną zapisując dane, które zostaną wykorzystane później w fazie pracy, gdzie dla zadanego punktu dana metoda wygeneruje odpowiadającą mu wartość bądź wartości aproksymowane. Funkcja aproksymująca może być przedstawiona w różnej postaci. Najczęściej jest to postać:Funkcje aproksymujące w postaci wielomianu i funkcji sklejanych można wykorzystać jedynie wtedy, gdy funkcja aproksymowana jest w postaci jednej zmiennej.zrodlo :www/ wikipedia.pl
była jak najmniejsza. Funkcja aproksymująca może wygładzać daną funkcję (gdy funkcja jest gładka, jest też różniczkowalna).Aproksymacja funkcji powoduje pojawienie się błędów, zwanych błędami aproksymacji. Dużą zaletą aproksymacji w stosunku do interpolacji jest to, że aby dobrze przybliżać, funkcja aproksymująca nie musi być wielomianem bardzo dużego stopnia (w ogóle nie musi być wielomianem). Przybliżenie w tym wypadku rozumiane jest jako minimalizacja pewnej funkcji błędu. Prawdopodobnie najpopularniejszą miarą tego błędu jest średni błąd kwadratowy, ale możliwe są również inne funkcje błędu, jak choćby błąd średni.Istnieje wiele metod aproksymacyjnych. Jednymi z najbardziej popularnych są: aproksymacja średniokwadratowa i aproksymacja jednostajna oraz aproksymacja liniowa, gdzie funkcją bazową jest funkcja liniowa.Wiele z metod aproksymacyjnych posiada fazę wstępną, zwaną również fazą uczenia oraz fazę pracy. W fazie wstępnej, metody te wykorzystując zadane pary punktów i odpowiadających im wartości aproksymacyjnych niejako „dostosowują” swoją strukturę wewnętrzną zapisując dane, które zostaną wykorzystane później w fazie pracy, gdzie dla zadanego punktu dana metoda wygeneruje odpowiadającą mu wartość bądź wartości aproksymowane. Funkcja aproksymująca może być przedstawiona w różnej postaci. Najczęściej jest to postać:Funkcje aproksymujące w postaci wielomianu i funkcji sklejanych można wykorzystać jedynie wtedy, gdy funkcja aproksymowana jest w postaci jednej zmiennej.zrodlo :www/ wikipedia.pl
poniedziałek, 12 listopada 2012
metody parabolistyczne i statystyka - zmienna losowa
POJĘCIE ZMIENNEJ LOSOWEJ
Podstawowe pojęcia rachunku prawdopodobieństwa:
- zdarzenie losowe,
- zdarzenie elementarne,
- prawdopodobieństwo,
- zbiór zdarzeń elementarnych.
Def. Niech E będzie zbiorem zdarzeń elementarnych danego doświadczenia. Funkcję X(e) przyporządkowującą każdemu zdarzeniu elementarnemu eEjedną i tylko jedną liczbę X(e)=x nazywamy zmienną losową.
Przykład: Z talii ciągniemy jedną kartę. Każdą kartę możnaponumerować, a więc można zdefiniować zmienną losową Xprzybierającą jedną z 52 wartości:x1 = 1, x2 = 2, . . . , x52 = 52.
TYPY ZMIENNYCH LOSOWYCH
Def. Zmienna losowa X jest typu skokowego, jeśli może przyjmować skończoną lub nieskończoną, ale przeliczalną liczbę wartości.
Wartości zmiennej losowej skokowej (określane często jako punkty skokowe) będziemy oznaczać przez x1, x2,..., natomiast prawdopodobieństwa, z jakimi są one realizowane (określane jako skoki), oznaczamy przez p1, p2,...
Def. Zmienna losowa X jest typu ciągłego, jeśli jej możliwe wartości tworzą przedział ze zbioru liczb rzeczywistych.
Dla zmiennej losowej typu ciągłego możliwe jest określenie prawdopodobieństwa, że przyjmuje ona wartość należącą do dowolnego zbioru jej wartości. Sposób rozdysponowania całej "masy" prawdopodobieństwa (równej 1) pomiędzy wartości, jakie przyjmuje dana zmienna losowa, określamy mianem jej rozkładu prawdopodobieństwa.
Zmienne losowe dzielimy na:
• ciągłe; zmienna przyjmuje dowolne wartości z określonego przedziału (w szczególności cały zbiór liczb rzeczywistych)
• skokowe (dyskretne); zmienna przyjmuje dowolne wartości ze zbioru przeliczalnego (np. zbiór liczb całkowitych z określonego przedziału)
Oznaczenia (analogicznie jak przy cechach statystycznych):
• duże litery (X, T, U, ...) - zmienna losowa
• małe litery (x, t, u, ...) - wartości zmiennej losowej
ROZKŁAD ZMIENNEJ LOSOWEJ SKOKOWEJ
Założenia:
- zmienna losowa X typu skokowego przyjmuje wartość x1, x2,... z prawdopodobieństwami, odpowiednio p1, p2,... ,
- prawdopodobieństwa p1, p2,... spełniają równość:
gdy zmienna losowa X przyjmuje skończoną liczbę n wielkości,
- prawdopodobieństwo p1, p2,... spełniają równość:
gdy zmienna losowa X przyjmuje nieskończoną liczbę wartości.
Def. Zbiór prawdopodobieństw postaci:
spełniających równość (1) lub (2) określamy mianem funkcji prawdopodobieństwa zmiennej losowej X typu skokowego.
Funkcję prawdopodobieństwa można przestawić tabelarycznie w poniższy sposób (przy założeniu, że zbiór wartości zmiennej losowej jest skończony):
xi
|
x1
|
x2
|
...
|
xn
|
pi
|
p1
|
p2
|
...
|
pn
|
Def. Dystrybuantą zmiennej losowej X nazywamy funkcję F(x) określoną na zbiorze liczb rzeczywistych jako:
F(x)=P(X<=x)
Własności dystrybuanty
a. P(X ≤ a) = F(a)
b. P(X ≥ a) = − F(a)
c. P(a ≤ X ≤ b) = F(b) − F(a)
Rozkłady zmiennych losowych dyskretnych.
I.
Rozkład dwumianowy (binomialny, Bernoulliego) dotyczy eksperymentu, w wyniku którego możemyotrzymać tylko jedno z dwóch wykluczających się zdarzeń:A - sukces (z prawdopodobieństwem p) lub A¯-niepowodzenie (z pr. q = 1 − p),I dośw. elementarne powtarzane jest niezależnie n razy.I rzut monetą (orzeł lub reszka),I test grupy osób na pewną chorobę (osoba zdrowa lubchora),I ankieta poparcia dla premiera (ankietowany popiera lubnie popiera),I stany różnych telefonów w centralce zakładowej ozadanej porze (numer zajęty lub wolny).
II.
Rozkład PoissonaP(X = k) = e−λ λkk!, λ > 0, k = 0, 1, 2, . . .I rozkład graniczny dla rozkładu dwumianowego przyn → ∞, p → 0,I stosowany w rozkładzie zjawisk rzadkich, np.I liczba błędów typograficznych w książce,I liczba samochodów uczestniczących danego dnia wkolizjach drogowych w dużym mieście,I liczba konfliktów w dostępie do zasobów w siecikomputerowej w ciągu 1 godziny,I liczba błędów lekarskich popełnionych w miesiącu wcałym szpitalu.
Rozkład geometryczny
P(X = k) = (1 − p)k−1p, k = 1, 2, 3, . . .I rozkład opisujący sytuację gdy powtarzamy doświadczenieBernoulliego aż do uzyskania pierwszego sukcesu,I liczba rzutów monetą, aż do uzyskania pierwszego orła,I liczba prób wysłania pakietu pocztą elektroniczną,I liczba prób automatycznego załączenia siecienergetycznej lub systemu zasilania po awarii.
Przykładowe zadanie z zastosowaniem zmiennej losowej
Rozpatrzmy dwukrotny rzut monetą. Niech zmienna losowa X charakteryzuje rzut pierwszy, a zmienna losowa Y - rzut drugi. Sprawdzić, czy te zmienne losowe są niezależne.
Rozwiązanie
- Mamy dwie zmienne losowe X i Y typu skokowego. Niech X(„Orzeł”)=Y(„Orzeł”)=1 i X(„Reszka”)=Y(„Reszka”)=0. Z natury rzutu monetą prawdopodobieństwo pojawienia się każdego ze zdarzeń dla pojedynczego rzutu jest równe i wynosi 0.5. Czyli P(X=0)=P(X=1)=P(Y=0)=P(Y=1)=0.5. Dla łącznej zmiennej losowej (X,Y) prawdopodobieństwo wypadnięcia każdego z czterech zdarzeń także jest równe i wynosi 0.25. Czyli P(X=0,Y=0)=P(X=1,Y=0)=P(X=0,Y=1)=P(X=1,Y=1)=0.25. Z definicji niezależności zmiennych losowych typu skokowego wynika, że:
- Gdzie rozkłady brzegowe definiowane są jako:
- W naszym przypadku:
- Wiemy, że:
- więc spełniona jest zależność:
metody numeryczne - Interpolacja wielomianowa
Interpolacja wielomianowa
Interpolacja wielomianowa, nazywana też interpolacją Lagrange'a, od nazwiska pioniera badań nad interpolacją Josepha Lagrange'a, lub po prostu interpolacją jest metodą numeryczną przybliżania funkcji tzw. wielomianem Lagrange'a stopnia n, przyjmującym w n+1 punktach, zwanych węzłami interpolacji wartości takie same jak przybliżana funkcja.
Interpolacja jest często stosowana w naukach doświadczalnych, gdzie dysponuje się zazwyczaj skończoną liczbą danych do określenia zależności między wielkościami.
Zgodnie z twierdzeniem Weierstrassa dowolną funkcję y=f(x) ciągłą na przedziale domkniętym można dowolnie przybliżyć za pomocą wielomianu odpowiednio wysokiego stopnia.
Znajdowanie odpowiedniego wielomianu
Wielomian przyjmujący zadane wartości w konkretnych punktach można zbudować w ten sposób:
- Dla pierwszego węzła o wartości
 znajduje się wielomian, który w tym punkcie przyjmuje wartość
znajduje się wielomian, który w tym punkcie przyjmuje wartość  , a w pozostałych węzłach
, a w pozostałych węzłach  wartość zero.
wartość zero. - Dla kolejnego węzła znajduje sie podobny wielomian, który w drugim węźle przyjmuje wartość
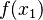 , a w pozostałych węzłach
, a w pozostałych węzłach  wartość zero.
wartość zero. - Dodaje się wartość ostatnio obliczonego wielomianu do wartości poprzedniego
- Dla każdego z pozostałych węzłów znajduje się podobny wielomian, za każdym razem dodając go do wielomianu wynikowego
- Wielomian będący sumą wielomianów obliczonych dla poszczególnych węzłów jest wielomianem interpolującym
Dowód ostatniego punktu i dokładny sposób tworzenia poszczególnych wielomianów opisany jest poniżej w dowodzie istnienia wielomianu interpolującego będącego podstawą algorytmu odnajdowania tego wielomianu.
Dowód istnienia wielomianu interpolującego
Niech  będą węzłami interpolacji funkcji
będą węzłami interpolacji funkcji 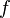 takimi, że znane są wartości
takimi, że znane są wartości 
Można zdefiniować funkcję:
 będą węzłami interpolacji funkcji
będą węzłami interpolacji funkcji 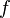 takimi, że znane są wartości
takimi, że znane są wartości 
Można zdefiniować funkcję:
 ,
, 
taką, że dla 
 jest wielomianem stopnia
jest wielomianem stopnia  (mianownik jest liczbą, a licznik iloczynem
(mianownik jest liczbą, a licznik iloczynem  wyrazów postaci
wyrazów postaci  )
)

 jest wielomianem stopnia
jest wielomianem stopnia  (mianownik jest liczbą, a licznik iloczynem
(mianownik jest liczbą, a licznik iloczynem  wyrazów postaci
wyrazów postaci  )
)- Gdy
 i
i  :
:
- Gdy
 i
i  :
:
(licznik = 0 ponieważ występuje element
 )
)Niech
 będzie wielomianem stopnia co najwyżej
będzie wielomianem stopnia co najwyżej  , określonym jako:
, określonym jako:Dla

 .
.
Wszystkie składniki sumy o indeksach różnych od
 są równe zeru (ponieważ dla
są równe zeru (ponieważ dla  , składnik o indeksie
, składnik o indeksie  jest równy:
jest równy: .
.
A więc
z czego wynika, że  jest wielomianem interpolującym funkcję
jest wielomianem interpolującym funkcję  w punktach
w punktach  .
.
 jest wielomianem interpolującym funkcję
jest wielomianem interpolującym funkcję  w punktach
w punktach  .
.Jednoznaczność interpolacji wielomianowej
Dowód
Załóżmy, że istnieją dwa tożsamościowo różne wielomiany  i
i  stopnia
stopnia  , przyjmujące w węzłach
, przyjmujące w węzłach  takie same wartości.
takie same wartości.
Niech
 i
i  stopnia
stopnia  , przyjmujące w węzłach
, przyjmujące w węzłach  takie same wartości.
takie same wartości.Niech
będzie wielomianem. Jest on stopnia co najwyżej
 (co wynika z własności odejmowania wielomianów).
(co wynika z własności odejmowania wielomianów).Ponieważ
 i
i  w węzłach
w węzłach  interpolują tę samą funkcję, to
interpolują tę samą funkcję, to  , a więc
, a więc  (węzły interpolacji są pierwiastkami
(węzły interpolacji są pierwiastkami  ).(*)
).(*)Ale każdy niezerowy wielomian stopnia
 ma co najwyżej
ma co najwyżej  pierwiastków rzeczywistych, a ponieważ z (*) wiadomo, że
pierwiastków rzeczywistych, a ponieważ z (*) wiadomo, że  ma
ma  pierwiastków, to
pierwiastków, to  musi być wielomian tożsamościowo równy zeru. A ponieważ
musi być wielomian tożsamościowo równy zeru. A ponieważ
to
co jest sprzeczne z założeniem, że
 i
i  są różne.
są różne.Błąd interpolacji
Dość naturalne wydaje się przyjęcie, że zwiększenie liczby węzłów interpolacji (lub stopnia wielomianu interpolacyjnego) pociąga za sobą coraz lepsze przybliżenie funkcji f(x) wielomianem  . Idealna byłaby zależność:
. Idealna byłaby zależność:
 . Idealna byłaby zależność:
. Idealna byłaby zależność: ,
,
tj. dla coraz większej liczby węzłów wielomian interpolacyjny staje się "coraz bardziej podobny" do interpolowanej funkcji.
Dla węzłów równo odległych tak być nie musi → efekt Rungego.
Można dowieść, że dla każdego wielomianu interpolacyjnego stopnia  , przybliżającego funkcję
, przybliżającego funkcję  w przedziale
w przedziale ![[a,b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) na podstawie
na podstawie  węzłów, istnieje taka liczba
węzłów, istnieje taka liczba  zależna od
zależna od  , że dla reszty interpolacji
, że dla reszty interpolacji 
 , przybliżającego funkcję
, przybliżającego funkcję  w przedziale
w przedziale ![[a,b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) na podstawie
na podstawie  węzłów, istnieje taka liczba
węzłów, istnieje taka liczba  zależna od
zależna od  , że dla reszty interpolacji
, że dla reszty interpolacji 
gdzie  , a
, a ![\xi \in [a;b]](http://upload.wikimedia.org/math/f/1/3/f1302a366e78b319c24f828cebac3bdc.png) jest liczbą zależną od x.
jest liczbą zależną od x.
 , a
, a ![\xi \in [a;b]](http://upload.wikimedia.org/math/f/1/3/f1302a366e78b319c24f828cebac3bdc.png) jest liczbą zależną od x.
jest liczbą zależną od x.
Do oszacowania z góry wartości  można posłużyć się wielomianami Czebyszewa stopnia
można posłużyć się wielomianami Czebyszewa stopnia  do oszacowania wartości
do oszacowania wartości  dla
dla ![x\in [-1,1]](http://upload.wikimedia.org/math/5/4/7/547db7d2339cfb3345123313fe6a4981.png) . Dla przedziału
. Dla przedziału ![[a,b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) wystarczy dokonać przeskalowania wielomianu
wystarczy dokonać przeskalowania wielomianu 
 można posłużyć się wielomianami Czebyszewa stopnia
można posłużyć się wielomianami Czebyszewa stopnia  do oszacowania wartości
do oszacowania wartości  dla
dla ![x\in [-1,1]](http://upload.wikimedia.org/math/5/4/7/547db7d2339cfb3345123313fe6a4981.png) . Dla przedziału
. Dla przedziału ![[a,b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) wystarczy dokonać przeskalowania wielomianu
wystarczy dokonać przeskalowania wielomianu 
Źródło : http://pl.wikipedia.org/wiki/Interpolacja_wielomianowa
Subskrybuj:
Komentarze (Atom)













