Układ równań liniowych – koniunkcja pewnej liczby (być może nieskończonej[1]) równań liniowych, czyli równań pierwszego rzędu.
Teoria układów równań liniowych jest działem algebry liniowej leżącej u podstaw nowoczesnej matematyki. Algorytmami obliczeniowymi zajmuje się dział nazywanynumeryczna algebra liniowa, same zaś metody odgrywają ważną rolę w inżynierii, fizyce, chemii, informatyce i ekonomii. Częstokroć aproksymuje (przybliża) się bardziej skomplikowane układy równań nieliniowych (opisujące modele matematyczne, czy symulacje komputerowe) dużo prostszymi układami równań liniowych (tzw.linearyzacja).
Układy równań liniowych rozpatruje się najczęściej nad ciałami (np. liczbami wymiernymi, rzeczywistymi, czy zespolonymi); choć ma to sens już w przypadku pierścieni(np. liczb całkowitych), to rozwiązywanie takich układów nastręcza znacznie więcej trudności (w szczególności oznacza to badanie modułów zamiast przestrzeni liniowych, zob. uogólnienia). W dalszej części przyjmuje się, że wszystkie współczynniki należą do ustalonego ciała.
Motywacje
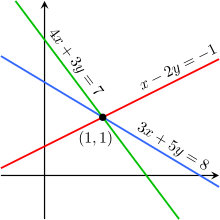
W geometrii euklidesowej można rozpatrywać miejsca geometryczne wyznaczone przez dane dwie proste na płaszczyźnie – mogą one wyznaczać prostą, punkt lub nie wyznaczać żadnego miejsca geometrycznego; odpowiada im odpowiednio nieskończony zbiór elementów, zbiór złożony z pojedynczego elementu lub zbiór pusty. Wprowadzenie na płaszczyźnie układu współrzędnych umożliwia algebraizację tego zadania: proste zadane są za pomocą równań liniowych, zaś miejsce geometryczne wyznaczone przez te proste odpowiada zbiorowi elementów spełniających wszystkie równania jednocześnie (pełną interpretację geometryczną można znaleźć w sekcjiUogólnienia).
Jeśli w układzie współrzędnych kartezjańskich proste  zadane są równaniami
zadane są równaniami
 zadane są równaniami
zadane są równaniami
oraz
to ich jedyny punkt wspólny  ma współrzędne
ma współrzędne  co łatwo sprawdzić wprost:
co łatwo sprawdzić wprost:
 ma współrzędne
ma współrzędne  co łatwo sprawdzić wprost:
co łatwo sprawdzić wprost:
To że jest to jedyny punkt wynika z faktu, iż proste te nie są równoległe (argument formalny podano dalej). Zwyczajowo równania prostych  zapisuje się bezpośrednio jedno pod drugim i spina klamrą:
zapisuje się bezpośrednio jedno pod drugim i spina klamrą:
 zapisuje się bezpośrednio jedno pod drugim i spina klamrą:
zapisuje się bezpośrednio jedno pod drugim i spina klamrą:
nazywając je układem równań liniowych, zaś zbiór elementów spełniających każde równanie z osobna (odpowiadający punktom wspólnym prostych) – jegorozwiązaniami.
Postać i zapis
Zobacz też: układ równań, równanie liniowe, wektor i macierz.
Niech  oznacza układ
oznacza układ 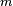 równań liniowych o
równań liniowych o  niewiadomych, tzn.
niewiadomych, tzn.
 oznacza układ
oznacza układ 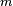 równań liniowych o
równań liniowych o  niewiadomych, tzn.
niewiadomych, tzn.
Niech  oraz
oraz  Wielkości
Wielkości  nazywa się niewiadomymi (lub zmiennymi), liczby
nazywa się niewiadomymi (lub zmiennymi), liczby  nazywa się współczynnikami, zaś elementy
nazywa się współczynnikami, zaś elementy  to wyrazy wolne. Układ nazywa się jednorodnym, jeżeli wyrazy wolne są równe zeru; inaczej mówiąc, wszystkie równania jednorodnego układu równań liniowych są jednorodne.
to wyrazy wolne. Układ nazywa się jednorodnym, jeżeli wyrazy wolne są równe zeru; inaczej mówiąc, wszystkie równania jednorodnego układu równań liniowych są jednorodne.
 oraz
oraz  Wielkości
Wielkości  nazywa się niewiadomymi (lub zmiennymi), liczby
nazywa się niewiadomymi (lub zmiennymi), liczby  nazywa się współczynnikami, zaś elementy
nazywa się współczynnikami, zaś elementy  to wyrazy wolne. Układ nazywa się jednorodnym, jeżeli wyrazy wolne są równe zeru; inaczej mówiąc, wszystkie równania jednorodnego układu równań liniowych są jednorodne.
to wyrazy wolne. Układ nazywa się jednorodnym, jeżeli wyrazy wolne są równe zeru; inaczej mówiąc, wszystkie równania jednorodnego układu równań liniowych są jednorodne.
Układ  można zapisać jako równanie wektorowe
można zapisać jako równanie wektorowe
 można zapisać jako równanie wektorowe
można zapisać jako równanie wektorowe
które można przedstawić w postaci
dzięki czemu każda niewiadoma może być postrzegana jako współczynnik kombinacji liniowej wektorów ![\scriptstyle \mathbf a_j = [a_{1j}, \dots, a_{mj}],](http://upload.wikimedia.org/math/2/2/d/22d5f167b3443d446a49f8ff4cd86968.png) tzn.
tzn.
![\scriptstyle \mathbf a_j = [a_{1j}, \dots, a_{mj}],](http://upload.wikimedia.org/math/2/2/d/22d5f167b3443d446a49f8ff4cd86968.png) tzn.
tzn.
gdzie ![\scriptstyle \mathbf b = [b_1, b_2, \dots, b_m]](http://upload.wikimedia.org/math/1/0/2/10207ecbbe0784d97d6ff450c8606151.png) nazywa się w tym kontekście wektorem wyrazów wolnych, zaś
nazywa się w tym kontekście wektorem wyrazów wolnych, zaś ![\scriptstyle \mathbf x = [x_1, x_2, \dots, x_n]](http://upload.wikimedia.org/math/4/1/8/4183c47e794346185233eabac01ae356.png) to wektor zmiennych (zob. uogólnienia).
to wektor zmiennych (zob. uogólnienia).
![\scriptstyle \mathbf b = [b_1, b_2, \dots, b_m]](http://upload.wikimedia.org/math/1/0/2/10207ecbbe0784d97d6ff450c8606151.png) nazywa się w tym kontekście wektorem wyrazów wolnych, zaś
nazywa się w tym kontekście wektorem wyrazów wolnych, zaś ![\scriptstyle \mathbf x = [x_1, x_2, \dots, x_n]](http://upload.wikimedia.org/math/4/1/8/4183c47e794346185233eabac01ae356.png) to wektor zmiennych (zob. uogólnienia).
to wektor zmiennych (zob. uogólnienia).
Korzystając z notacji macierzowej układ  można przedstawić w postaci
można przedstawić w postaci
 można przedstawić w postaci
można przedstawić w postaci
co, przy pomocy standardowego mnożenia macierzy, można zapisać w formie
Innymi słowy dowolny układ  można traktować jak macierzowe równanie liniowe
można traktować jak macierzowe równanie liniowe
 można traktować jak macierzowe równanie liniowe
można traktować jak macierzowe równanie liniowe
gdzie ![\scriptstyle \mathbf A = [a_{ij}]](http://upload.wikimedia.org/math/0/4/2/0428633fe6c561576a3b711595cfa9a7.png) jest macierzą typu
jest macierzą typu  zaś
zaś ![\scriptstyle \mathbf X = [x_j]](http://upload.wikimedia.org/math/7/7/7/777682be1d606c68b05cad262619fda2.png) oraz
oraz ![\scriptstyle \mathbf B = [b_i]](http://upload.wikimedia.org/math/4/6/0/460dd5590f2887f6d83a1a3688d54e0f.png) to macierze odpowiednio typów
to macierze odpowiednio typów  oraz
oraz  Macierz
Macierz  nazywa się macierzą główną układu
nazywa się macierzą główną układu Jeśli macierz układu jest kwadratowa, tzn.
Jeśli macierz układu jest kwadratowa, tzn.  to sam układ również nazywa się czasem kwadratowym, jeśli jest ona prostokątna, czyli
to sam układ również nazywa się czasem kwadratowym, jeśli jest ona prostokątna, czyli  to układ także nazywa się niekiedy prostokątnym.
to układ także nazywa się niekiedy prostokątnym.
![\scriptstyle \mathbf A = [a_{ij}]](http://upload.wikimedia.org/math/0/4/2/0428633fe6c561576a3b711595cfa9a7.png) jest macierzą typu
jest macierzą typu  zaś
zaś ![\scriptstyle \mathbf X = [x_j]](http://upload.wikimedia.org/math/7/7/7/777682be1d606c68b05cad262619fda2.png) oraz
oraz ![\scriptstyle \mathbf B = [b_i]](http://upload.wikimedia.org/math/4/6/0/460dd5590f2887f6d83a1a3688d54e0f.png) to macierze odpowiednio typów
to macierze odpowiednio typów  oraz
oraz  Macierz
Macierz  nazywa się macierzą główną układu
nazywa się macierzą główną układu Jeśli macierz układu jest kwadratowa, tzn.
Jeśli macierz układu jest kwadratowa, tzn.  to sam układ również nazywa się czasem kwadratowym, jeśli jest ona prostokątna, czyli
to sam układ również nazywa się czasem kwadratowym, jeśli jest ona prostokątna, czyli  to układ także nazywa się niekiedy prostokątnym.
to układ także nazywa się niekiedy prostokątnym.
Ponieważ macierz  w powyższym równaniu macierzowym zachowuje się przy operacjach elementarnych na wierszach (każde równanie jest kombinacją liniowąelementów
w powyższym równaniu macierzowym zachowuje się przy operacjach elementarnych na wierszach (każde równanie jest kombinacją liniowąelementów  ), to wygodne jest pominięcie go w zapisie i rozpatrywanie macierzy rozszerzonej bądź uzupełnionej układu
), to wygodne jest pominięcie go w zapisie i rozpatrywanie macierzy rozszerzonej bądź uzupełnionej układu  złożonej z elementów macierzy
złożonej z elementów macierzy  oraz
oraz  w której wyrazy
w której wyrazy  oddziela się zwykle optycznie od wyrazów
oddziela się zwykle optycznie od wyrazów  pionową kreską:
pionową kreską:
 w powyższym równaniu macierzowym zachowuje się przy operacjach elementarnych na wierszach (każde równanie jest kombinacją liniowąelementów
w powyższym równaniu macierzowym zachowuje się przy operacjach elementarnych na wierszach (każde równanie jest kombinacją liniowąelementów  ), to wygodne jest pominięcie go w zapisie i rozpatrywanie macierzy rozszerzonej bądź uzupełnionej układu
), to wygodne jest pominięcie go w zapisie i rozpatrywanie macierzy rozszerzonej bądź uzupełnionej układu  złożonej z elementów macierzy
złożonej z elementów macierzy  oraz
oraz  w której wyrazy
w której wyrazy  oddziela się zwykle optycznie od wyrazów
oddziela się zwykle optycznie od wyrazów  pionową kreską:
pionową kreską:
Macierz  może być traktowana jako przypadek szczególny macierzy rozszerzonej, w której wyrazy
może być traktowana jako przypadek szczególny macierzy rozszerzonej, w której wyrazy  są równe zeru.
są równe zeru.
 może być traktowana jako przypadek szczególny macierzy rozszerzonej, w której wyrazy
może być traktowana jako przypadek szczególny macierzy rozszerzonej, w której wyrazy  są równe zeru.
są równe zeru.
Dowolny układ  można zapisać w postaci
można zapisać w postaci
 można zapisać w postaci
można zapisać w postaci
co w zapisie macierzowym można ująć następująco:
W ten sposób układ  w postaci
w postaci  można zapisać jako
można zapisać jako
 w postaci
w postaci  można zapisać jako
można zapisać jako
gdzie  jest macierzą typu
jest macierzą typu  zaś
zaś  jest macierzą typu
jest macierzą typu  a
a  jest macierzą zerową typu
jest macierzą zerową typu  Macierz główna
Macierz główna  układu
układu  jest więc formalnie macierzą rozszerzoną układu
jest więc formalnie macierzą rozszerzoną układu  Oznacza to, że układ niejednorodny
Oznacza to, że układ niejednorodny  zmiennych można sprowadzić do układu jednorodnego
zmiennych można sprowadzić do układu jednorodnego  zmiennych, przy czym jedna z nich jest ustalona (zob. uogólnienia).
zmiennych, przy czym jedna z nich jest ustalona (zob. uogólnienia).
 jest macierzą typu
jest macierzą typu  zaś
zaś  jest macierzą typu
jest macierzą typu  a
a  jest macierzą zerową typu
jest macierzą zerową typu  Macierz główna
Macierz główna  układu
układu  jest więc formalnie macierzą rozszerzoną układu
jest więc formalnie macierzą rozszerzoną układu  Oznacza to, że układ niejednorodny
Oznacza to, że układ niejednorodny  zmiennych można sprowadzić do układu jednorodnego
zmiennych można sprowadzić do układu jednorodnego  zmiennych, przy czym jedna z nich jest ustalona (zob. uogólnienia).
zmiennych, przy czym jedna z nich jest ustalona (zob. uogólnienia).Rozwiązania
- układ niedookreślony, który ma mniej równań niż niewiadomych,
 zwykle jest nieoznaczony;
zwykle jest nieoznaczony; - układ nadokreślony mający więcej równań niż niewiadomych,
 zazwyczaj jest sprzeczny;
zazwyczaj jest sprzeczny; - układ, który ma tyle równań co niewiadomych,
 często ma jedno rozwiązanie.
często ma jedno rozwiązanie.
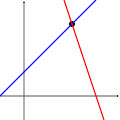
Przypadki te obrazują następujące wykresy dla układów równań liniowych dwóch zmiennych:
Operacje elementarne
Osobny artykuł: operacje elementarne.
Podstawową metodą rozwiązywania układów równań jest przekształcanie danego układu w inny, który ma ten sam zbiór rozwiązań – układy takie nazywa się równoważnymi. Można wyróżnić trzyoperacje elementarne na wierszach przekształcające dany układ w układ do niego równoważny:
- dodanie do równania innego równania pomnożonego przez liczbę,
- zamiana dwóch równań miejscami,
- pomnożenie równania przez liczbę różną od zera.
Powszechnie stosowanymi metodami rozwiązywania układów równań liniowych za pomocą wspomnianych operacji elementarnych są:
- metoda eliminacji Gaussa, w której układ przekształca się do równoważnego z nim układu równań z rosnącą liczbą zmiennych;
- metoda eliminacji Gaussa-Jordana, w której układ przekształca się dalej (poprzez kolejne podstawienia równań z mniejszą liczbą zmiennych do tych z większą) do równoważnego z nim układu równań liniowych wiążących bezpośrednio każdą zmienną z pewną wartością.
Oba algorytmy opisano w przypadku, gdy układ jest oznaczony. Jeśli układ jest sprzeczny, to uzyskuje się (co najmniej jedno) równanie sprzeczne, które mówi o sprzeczności całego układu. Jeśli układ jest nieoznaczony, to niektóre zmienne przenosi się do prawych części równań i rozwiązanie podaje się w postaci wyrażania jednych zmiennych przez inne (zob. też następną podsekcję). Metody te w zapisie macierzowym odpowiadają (zwykle) najefektywniejszym metodom przekształcania macierzy głównej (w przypadku jednorodnym) lub rozszerzonej (w przypadku niejednorodnym) układu do wierszowo z nią równoważnej macierzy schodkowej w metodzie Gaussa i macierzy schodkowej zredukowanej w metodzie Gaussa-Jordana.
Opis ogólny i zależność
Zobacz też: zmienne zależna i niezależna, liniowa niezależność i twierdzenie o rzędzie.
Jeżeli układ ma więcej niż jedno rozwiązanie, to można je scharakteryzować podając tzw. rozwiązanie ogólne układu, będące w istocie układem równań w prostej postaci − w przypadku jeśli układ ma jedno rozwiązanie, to rozwiązanie można odczytać wprost z rozwiązania ogólnego. Układ
gdzie  a zmienne
a zmienne  nie występują po prawej stronie równań (tzn.
nie występują po prawej stronie równań (tzn.  dla
dla  ) zadaje rozwiązanie ogólne układu
) zadaje rozwiązanie ogólne układu  (krótko:
(krótko:  jest rozwiązaniem ogólnym układu
jest rozwiązaniem ogólnym układu  ). Zmienne
). Zmienne  nazywa się wtedy zależnymi, a pozostałe
nazywa się wtedy zależnymi, a pozostałe 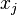 nazywa się wówczas zmiennymi niezależnymi (alboparametrami).
nazywa się wówczas zmiennymi niezależnymi (alboparametrami).
 a zmienne
a zmienne  nie występują po prawej stronie równań (tzn.
nie występują po prawej stronie równań (tzn.  dla
dla  ) zadaje rozwiązanie ogólne układu
) zadaje rozwiązanie ogólne układu  (krótko:
(krótko:  jest rozwiązaniem ogólnym układu
jest rozwiązaniem ogólnym układu  ). Zmienne
). Zmienne  nazywa się wtedy zależnymi, a pozostałe
nazywa się wtedy zależnymi, a pozostałe 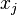 nazywa się wówczas zmiennymi niezależnymi (alboparametrami).
nazywa się wówczas zmiennymi niezależnymi (alboparametrami).
Równania w układzie liniowym nazywa się niezależnymi, jeśli żadne z nich nie może być uzyskane z innych za pomocą operacji elementarnych. Innymi słowy każde z nich zawiera nową informację o zmiennych i usunięcie któregokolwiek z nich powiększa liczbę rozwiązań; w przypadku równań liniowych niezależność ta nazywana jest niezależnością liniową (zob. charakteryzacja).
Wzory Cramera
Zobacz też: wzory Cramera.
Jeśli macierz główna układu jest kwadratowa (układ jest kwadratowy), to oznaczoność układu jest równoważna odwracalności jego macierzy głównej. Macierz jest odwracalna wtedy i tylko wtedy, gdy jest nieosobliwa, tzn. ma niezerowy wyznacznik. Wówczas mnożąc z lewej strony (w ogólności mnożenie macierzy nie jest przemienne) równanie
przez macierz  czyli
czyli  otrzymuje się rozwiązanie
otrzymuje się rozwiązanie
 czyli
czyli  otrzymuje się rozwiązanie
otrzymuje się rozwiązanie
Macierz odwrotną do  można wyznaczyć w dowolny sposób, np. korzystając z operacji elementarnych, bądź obliczając iloraz macierzy dołączonej
można wyznaczyć w dowolny sposób, np. korzystając z operacji elementarnych, bądź obliczając iloraz macierzy dołączonej  przez wyznacznik macierzy
przez wyznacznik macierzy  Pierwsza metoda odpowiada w istocie metodzie eliminacji Gaussa-Jordana, druga z kolei jest wnioskiem z twierdzenia Cramera:
Pierwsza metoda odpowiada w istocie metodzie eliminacji Gaussa-Jordana, druga z kolei jest wnioskiem z twierdzenia Cramera:
 można wyznaczyć w dowolny sposób, np. korzystając z operacji elementarnych, bądź obliczając iloraz macierzy dołączonej
można wyznaczyć w dowolny sposób, np. korzystając z operacji elementarnych, bądź obliczając iloraz macierzy dołączonej  przez wyznacznik macierzy
przez wyznacznik macierzy  Pierwsza metoda odpowiada w istocie metodzie eliminacji Gaussa-Jordana, druga z kolei jest wnioskiem z twierdzenia Cramera:
Pierwsza metoda odpowiada w istocie metodzie eliminacji Gaussa-Jordana, druga z kolei jest wnioskiem z twierdzenia Cramera:
wtedy też, na mocy rozwinięcia Laplace'a, wzory na elementy  powyższej macierzy, nazywane właśnie wzorami Cramera, dane są jako ilorazy wyznaczników macierzy
powyższej macierzy, nazywane właśnie wzorami Cramera, dane są jako ilorazy wyznaczników macierzy  przez wyznacznik macierzy głównej
przez wyznacznik macierzy głównej  układu
układu 
 powyższej macierzy, nazywane właśnie wzorami Cramera, dane są jako ilorazy wyznaczników macierzy
powyższej macierzy, nazywane właśnie wzorami Cramera, dane są jako ilorazy wyznaczników macierzy  przez wyznacznik macierzy głównej
przez wyznacznik macierzy głównej  układu
układu 
gdzie  oznacza macierz powstałą z
oznacza macierz powstałą z  poprzez zamianę elementów
poprzez zamianę elementów  -tej kolumny elementami macierzy wyrazów wolnych
-tej kolumny elementami macierzy wyrazów wolnych  o ile tylko
o ile tylko  nie jest równy zeru.
nie jest równy zeru.
 oznacza macierz powstałą z
oznacza macierz powstałą z  poprzez zamianę elementów
poprzez zamianę elementów  -tej kolumny elementami macierzy wyrazów wolnych
-tej kolumny elementami macierzy wyrazów wolnych  o ile tylko
o ile tylko  nie jest równy zeru.
nie jest równy zeru.
Jak już wspomniano, układ jest oznaczony, gdy macierz główna jest odwracalna. Jeżeli wyznacznik macierzy głównej nie jest niezerowy, to układ jest sprzeczny, gdy którykolwiek z wyznaczników  jest niezerowy. Twierdzenie odwrotne nie jest prawdziwe: jeśli wszystkie wyznaczniki są zerowe, to układ nie musi być nieoznaczony (wiadomo jedynie, że nie jest oznaczony, czyli może być tak sprzeczny, jak i nieoznaczony).
jest niezerowy. Twierdzenie odwrotne nie jest prawdziwe: jeśli wszystkie wyznaczniki są zerowe, to układ nie musi być nieoznaczony (wiadomo jedynie, że nie jest oznaczony, czyli może być tak sprzeczny, jak i nieoznaczony).
 jest niezerowy. Twierdzenie odwrotne nie jest prawdziwe: jeśli wszystkie wyznaczniki są zerowe, to układ nie musi być nieoznaczony (wiadomo jedynie, że nie jest oznaczony, czyli może być tak sprzeczny, jak i nieoznaczony).
jest niezerowy. Twierdzenie odwrotne nie jest prawdziwe: jeśli wszystkie wyznaczniki są zerowe, to układ nie musi być nieoznaczony (wiadomo jedynie, że nie jest oznaczony, czyli może być tak sprzeczny, jak i nieoznaczony).
Stosowanie wzorów Cramera do rozwiązywania „konkretnych” układów wymaga z reguły więcej obliczeń niż stosowanie metody Gaussa, jednak metoda Cramera bywa dogodniejsza w rozważaniach teoretycznych.
Inne metody[edytuj]
Układy trzech, czy nawet czterech zmiennych łatwo rozwiązać ręcznie (najlepiej metodą Gaussa); do większych stosuje się często komputery. Standardowe podejście opiera się na metodzie eliminacji Gaussa. Bardzo ważne jest unikanie dzielenia przez małe liczby, które może prowadzić do błędów zaokrągleń – można to osiągnąć poprzez zmianę kolejności równań (druga operacja elementarna). Ponadto, w szczególnym przypadku, gdy dane układy mają tę samą macierz główną, lecz różne macierze rozszerzone (tzn. układy mają te same współczynniki, lecz różne wyrazy wolne), to pomocne okazuje się wyznaczenie rozkładu LU macierzy głównej.
Często możliwe jest wykorzystanie szczególnej postaci macierzy głównej układu do uzyskania szybszych bądź dokładniejszych algorytmów. Przykładowo układy z symetrycznymi i dodatnio określonymimacierzami głównymi mogą być rozwiązane dużo szybciej za pomocą rozkładu Cholesky'ego. Rekursja Levinsona jest z kolei szybką metodą rozwiązywania układów opisanych macierzą Toeplitza. Istnieją także specjalne metody dla macierzy z wieloma zerami (tzw. macierzy rzadkich), które pojawiają się często w zastosowaniach matematyki.
W zupełnie inny sposób podchodzi się do bardzo dużych układów, których rozwiązanie kosztowałoby zbyt dużo czasu lub pamięci. Idea polega na rozpoczęciu od wstępnego przybliżenia rozwiązania (które wcale nie musi być dokładne) i stopniowym jego poprawianiu – jeśli jest ono wystarczająco dokładne, właśnie ono przyjmowane jest jako rozwiązanie układu. Tego rodzaju podejście prowadzi metod iteracyjnych.
Charakteryzacja
Osobne artykuły: rząd i twierdzenie Kroneckera-Capellego.
O niesprzeczności i liczbie rozwiązań układu 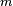 równań liniowych o
równań liniowych o  niewiadomych mówi twierdzenie Kroneckera-Capellego: ma on rozwiązanie wtedy i tylko wtedy, gdy rząd
niewiadomych mówi twierdzenie Kroneckera-Capellego: ma on rozwiązanie wtedy i tylko wtedy, gdy rząd  macierzy głównej tego układu jest równy rzędowi
macierzy głównej tego układu jest równy rzędowi  jego macierzy rozszerzonej. Układ jednorodny zawsze ma rozwiązanie trywialne, tzn. postaci
jego macierzy rozszerzonej. Układ jednorodny zawsze ma rozwiązanie trywialne, tzn. postaci  jest to jedyne rozwiązanie oznaczonego układu jednorodnego. Układ niesprzeczny jest
jest to jedyne rozwiązanie oznaczonego układu jednorodnego. Układ niesprzeczny jest
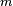 równań liniowych o
równań liniowych o  niewiadomych mówi twierdzenie Kroneckera-Capellego: ma on rozwiązanie wtedy i tylko wtedy, gdy rząd
niewiadomych mówi twierdzenie Kroneckera-Capellego: ma on rozwiązanie wtedy i tylko wtedy, gdy rząd  macierzy głównej tego układu jest równy rzędowi
macierzy głównej tego układu jest równy rzędowi  jego macierzy rozszerzonej. Układ jednorodny zawsze ma rozwiązanie trywialne, tzn. postaci
jego macierzy rozszerzonej. Układ jednorodny zawsze ma rozwiązanie trywialne, tzn. postaci  jest to jedyne rozwiązanie oznaczonego układu jednorodnego. Układ niesprzeczny jest
jest to jedyne rozwiązanie oznaczonego układu jednorodnego. Układ niesprzeczny jest- oznaczony, tzn. ma jedno rozwiązanie, gdy rząd macierz głównej układu jest równy liczbie niewiadomych;
- nieoznaczony, tzn. nieskończenie wiele rozwiązań, gdy rząd macierzy głównej układu jest mniejszy od liczby niewiadomych – zbiór rozwiązań zależy wtedy od
 parametrów.
parametrów.
Z punktu widzenia geometrii analitycznej rozwiązania układu tworzą przestrzeń liniową (w przypadku jednorodnym) albo przestrzeń afiniczną (w przypadku niejednorodnym) wymiaru  W szczególności więc, jeśli
W szczególności więc, jeśli  to rozwiązaniem jest punkt.
to rozwiązaniem jest punkt.
 W szczególności więc, jeśli
W szczególności więc, jeśli  to rozwiązaniem jest punkt.
to rozwiązaniem jest punkt.
Niech  oznacza zbiór rozwiązań układu jednorodnego
oznacza zbiór rozwiązań układu jednorodnego  Ponieważ układ jest jednorodny, to
Ponieważ układ jest jednorodny, to  nie jest pusty. Niech
nie jest pusty. Niech  należą do
należą do  tzn.
tzn.  oraz
oraz  skąd
skąd  czyli
czyli  również należy do
również należy do  a więc
a więc  jest podprzestrzenią liniową przestrzeni współrzędnych. Ponieważ przekształcenie macierzy układu do postaci schodkowej zredukowanej nie zmienia zbioru rozwiązań
jest podprzestrzenią liniową przestrzeni współrzędnych. Ponieważ przekształcenie macierzy układu do postaci schodkowej zredukowanej nie zmienia zbioru rozwiązań  układu, to pierwsze
układu, to pierwsze  wierszy jest kombinacją liniowąostatnich
wierszy jest kombinacją liniowąostatnich  liniowo niezależnych wierszy; w ten sposób również
liniowo niezależnych wierszy; w ten sposób również  kolumn tej macierzy tworzy bazę przestrzeni
kolumn tej macierzy tworzy bazę przestrzeni  (w gruncie rzeczy wykorzystuje się tu pojęcie rzędu; w ogólności powyższe obserwacje są równoważne twierdzeniu o rzędzie przekształcenia liniowego).
(w gruncie rzeczy wykorzystuje się tu pojęcie rzędu; w ogólności powyższe obserwacje są równoważne twierdzeniu o rzędzie przekształcenia liniowego).
 oznacza zbiór rozwiązań układu jednorodnego
oznacza zbiór rozwiązań układu jednorodnego  Ponieważ układ jest jednorodny, to
Ponieważ układ jest jednorodny, to  nie jest pusty. Niech
nie jest pusty. Niech  należą do
należą do  tzn.
tzn.  oraz
oraz  skąd
skąd  czyli
czyli  również należy do
również należy do  a więc
a więc  jest podprzestrzenią liniową przestrzeni współrzędnych. Ponieważ przekształcenie macierzy układu do postaci schodkowej zredukowanej nie zmienia zbioru rozwiązań
jest podprzestrzenią liniową przestrzeni współrzędnych. Ponieważ przekształcenie macierzy układu do postaci schodkowej zredukowanej nie zmienia zbioru rozwiązań  układu, to pierwsze
układu, to pierwsze  wierszy jest kombinacją liniowąostatnich
wierszy jest kombinacją liniowąostatnich  liniowo niezależnych wierszy; w ten sposób również
liniowo niezależnych wierszy; w ten sposób również  kolumn tej macierzy tworzy bazę przestrzeni
kolumn tej macierzy tworzy bazę przestrzeni  (w gruncie rzeczy wykorzystuje się tu pojęcie rzędu; w ogólności powyższe obserwacje są równoważne twierdzeniu o rzędzie przekształcenia liniowego).
(w gruncie rzeczy wykorzystuje się tu pojęcie rzędu; w ogólności powyższe obserwacje są równoważne twierdzeniu o rzędzie przekształcenia liniowego).
Teraz niech  będzie zbiorem rozwiązań układu niejednorodnego
będzie zbiorem rozwiązań układu niejednorodnego  ponieważ
ponieważ  to zbiór ten nie jest pusty. Niech
to zbiór ten nie jest pusty. Niech  będzie ustalonym rozwiązaniem, a
będzie ustalonym rozwiązaniem, a  dowolnym rozwiązaniem układu; wówczas z
dowolnym rozwiązaniem układu; wówczas z  oraz
oraz  wynika
wynika  czyli
czyli  należy do zbioru
należy do zbioru  rozwiązań odpowiadającego mu układu jednorodnego. Wraz z nim do
rozwiązań odpowiadającego mu układu jednorodnego. Wraz z nim do  należy również rozwiązanie przeciwne
należy również rozwiązanie przeciwne  skąd
skąd  co wobec dowolności
co wobec dowolności  oznacza
oznacza  Jeśli zaś
Jeśli zaś  gdzie
gdzie  należy do
należy do  a
a  należy do
należy do  to
to  czyli
czyli  należy do
należy do  a więc
a więc  Wynika stąd, że zbiór rozwiązań układu niejednorodnego jest warstwą podprzestrzeni liniowej rozwiązań odpowiadającego mu układu jednorodnego, zatem jest podprzestrzenią afiniczną tej samej przestrzeni współrzędnych.
Wynika stąd, że zbiór rozwiązań układu niejednorodnego jest warstwą podprzestrzeni liniowej rozwiązań odpowiadającego mu układu jednorodnego, zatem jest podprzestrzenią afiniczną tej samej przestrzeni współrzędnych.
 będzie zbiorem rozwiązań układu niejednorodnego
będzie zbiorem rozwiązań układu niejednorodnego  ponieważ
ponieważ  to zbiór ten nie jest pusty. Niech
to zbiór ten nie jest pusty. Niech  będzie ustalonym rozwiązaniem, a
będzie ustalonym rozwiązaniem, a  dowolnym rozwiązaniem układu; wówczas z
dowolnym rozwiązaniem układu; wówczas z  oraz
oraz  wynika
wynika  czyli
czyli  należy do zbioru
należy do zbioru  rozwiązań odpowiadającego mu układu jednorodnego. Wraz z nim do
rozwiązań odpowiadającego mu układu jednorodnego. Wraz z nim do  należy również rozwiązanie przeciwne
należy również rozwiązanie przeciwne  skąd
skąd  co wobec dowolności
co wobec dowolności  oznacza
oznacza  Jeśli zaś
Jeśli zaś  gdzie
gdzie  należy do
należy do  a
a  należy do
należy do  to
to  czyli
czyli  należy do
należy do  a więc
a więc  Wynika stąd, że zbiór rozwiązań układu niejednorodnego jest warstwą podprzestrzeni liniowej rozwiązań odpowiadającego mu układu jednorodnego, zatem jest podprzestrzenią afiniczną tej samej przestrzeni współrzędnych.
Wynika stąd, że zbiór rozwiązań układu niejednorodnego jest warstwą podprzestrzeni liniowej rozwiązań odpowiadającego mu układu jednorodnego, zatem jest podprzestrzenią afiniczną tej samej przestrzeni współrzędnych.Uogólnienia
Z punktu widzenia geometrii analitycznej układ 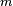 równań o
równań o  zmiennych odpowiada zadaniu
zmiennych odpowiada zadaniu 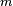 hiperpłaszczyzn w
hiperpłaszczyzn w  -wymiarowej przestrzeni liniowej (lubprzestrzeni afinicznej), rozwiązaniem (ogólnym) jest wtedy przestrzeń będąca częścią wspólną wszystkich hiperpłaszczyzn.
-wymiarowej przestrzeni liniowej (lubprzestrzeni afinicznej), rozwiązaniem (ogólnym) jest wtedy przestrzeń będąca częścią wspólną wszystkich hiperpłaszczyzn.
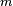 równań o
równań o  zmiennych odpowiada zadaniu
zmiennych odpowiada zadaniu 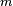 hiperpłaszczyzn w
hiperpłaszczyzn w  -wymiarowej przestrzeni liniowej (lubprzestrzeni afinicznej), rozwiązaniem (ogólnym) jest wtedy przestrzeń będąca częścią wspólną wszystkich hiperpłaszczyzn.
-wymiarowej przestrzeni liniowej (lubprzestrzeni afinicznej), rozwiązaniem (ogólnym) jest wtedy przestrzeń będąca częścią wspólną wszystkich hiperpłaszczyzn.
Stosując notację wektorową można wykorzystać do opisu układów równań liniowych cały aparat algebry liniowej. Zbiór wszystkich kombinacji liniowych układu wektorów nazywa się powłoką liniową; w ten sposób układ równań ma rozwiązanie, jeśli wektor  leży w powłoce generowanej przez wektory
leży w powłoce generowanej przez wektory  Jeżeli każdy wektor powłoki można wyrazić jednoznacznie jako kombinację liniową wektorów
Jeżeli każdy wektor powłoki można wyrazić jednoznacznie jako kombinację liniową wektorów  to układ jest oznaczony. W każdej powłoce można wyróżnić bazę złożoną zliniowo niezależnych wektorów, dzięki którym wspomniane wyrażenie może być jednoznaczne; liczba wektorów w bazie (wymiar) nie może być większy niż
to układ jest oznaczony. W każdej powłoce można wyróżnić bazę złożoną zliniowo niezależnych wektorów, dzięki którym wspomniane wyrażenie może być jednoznaczne; liczba wektorów w bazie (wymiar) nie może być większy niż  czy
czy  ale może być mniejsza. Rozwiązanie istnieje, gdy powłoka składa się z
ale może być mniejsza. Rozwiązanie istnieje, gdy powłoka składa się z 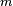 liniowo niezależnych wektorów.
liniowo niezależnych wektorów.
 leży w powłoce generowanej przez wektory
leży w powłoce generowanej przez wektory  Jeżeli każdy wektor powłoki można wyrazić jednoznacznie jako kombinację liniową wektorów
Jeżeli każdy wektor powłoki można wyrazić jednoznacznie jako kombinację liniową wektorów  to układ jest oznaczony. W każdej powłoce można wyróżnić bazę złożoną zliniowo niezależnych wektorów, dzięki którym wspomniane wyrażenie może być jednoznaczne; liczba wektorów w bazie (wymiar) nie może być większy niż
to układ jest oznaczony. W każdej powłoce można wyróżnić bazę złożoną zliniowo niezależnych wektorów, dzięki którym wspomniane wyrażenie może być jednoznaczne; liczba wektorów w bazie (wymiar) nie może być większy niż  czy
czy  ale może być mniejsza. Rozwiązanie istnieje, gdy powłoka składa się z
ale może być mniejsza. Rozwiązanie istnieje, gdy powłoka składa się z 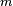 liniowo niezależnych wektorów.
liniowo niezależnych wektorów.
Najogólniejszą postacią przekształcenia liniowego  między dwoma przestrzeniami liniowymi jest kombinacja liniowa zadających go wektorów
między dwoma przestrzeniami liniowymi jest kombinacja liniowa zadających go wektorów  (zob. twierdzenie o przekształceniu liniowym zadanym na bazie). Samo przekształcenie liniowe
(zob. twierdzenie o przekształceniu liniowym zadanym na bazie). Samo przekształcenie liniowe  przy ustalonych bazach dziedziny i przeciwdziedziny, można zapisać w postaci macierzy
przy ustalonych bazach dziedziny i przeciwdziedziny, można zapisać w postaci macierzy ![\scriptstyle \mathbf A = [\mathbf a_j].](http://upload.wikimedia.org/math/2/e/3/2e38b797329f73a654ba5121691ed76a.png) Wówczas obliczaniu wartości
Wówczas obliczaniu wartości  odpowiada mnożenie
odpowiada mnożenie  a rozwiązywanie układu równań jednorodnych jest w istocie wyznaczaniem miejsc zerowych przekształcenia liniowego
a rozwiązywanie układu równań jednorodnych jest w istocie wyznaczaniem miejsc zerowych przekształcenia liniowego  Przedstawione w poprzedniej sekcji rozumowanie jest przypadkiem szczególnym ogólnego wyniku – zbiór miejsc zerowych przekształcenia liniowego, nazywany jego jądrem, tworzy podprzestrzeń liniową w dziedzinie tego przekształcenia. Wymiar powłoki wspomniany w poprzednim akapicie w przypadku macierzy nazywa się jej rzędem (wierszowym). W ten sposób układ równań liniowych
Przedstawione w poprzedniej sekcji rozumowanie jest przypadkiem szczególnym ogólnego wyniku – zbiór miejsc zerowych przekształcenia liniowego, nazywany jego jądrem, tworzy podprzestrzeń liniową w dziedzinie tego przekształcenia. Wymiar powłoki wspomniany w poprzednim akapicie w przypadku macierzy nazywa się jej rzędem (wierszowym). W ten sposób układ równań liniowych  można traktować jako problem opisu przekształcenia liniowego
można traktować jako problem opisu przekształcenia liniowego  przy czym istnienie rozwiązań jest tożsame z należeniem
przy czym istnienie rozwiązań jest tożsame z należeniem  do obrazu
do obrazu  (czyli istnieniem takiego wektora
(czyli istnieniem takiego wektora  który spełniałby
który spełniałby  ), a ich jednoznaczność jest równoważna trywialności jądra
), a ich jednoznaczność jest równoważna trywialności jądra  (czyli różnowartościowości przekształcenia). Zależność między wymiarami jądra i obrazu opisuje tzw. twierdzenie o rzędzie przekształcenia liniowego.
(czyli różnowartościowości przekształcenia). Zależność między wymiarami jądra i obrazu opisuje tzw. twierdzenie o rzędzie przekształcenia liniowego.
 między dwoma przestrzeniami liniowymi jest kombinacja liniowa zadających go wektorów
między dwoma przestrzeniami liniowymi jest kombinacja liniowa zadających go wektorów  (zob. twierdzenie o przekształceniu liniowym zadanym na bazie). Samo przekształcenie liniowe
(zob. twierdzenie o przekształceniu liniowym zadanym na bazie). Samo przekształcenie liniowe  przy ustalonych bazach dziedziny i przeciwdziedziny, można zapisać w postaci macierzy
przy ustalonych bazach dziedziny i przeciwdziedziny, można zapisać w postaci macierzy ![\scriptstyle \mathbf A = [\mathbf a_j].](http://upload.wikimedia.org/math/2/e/3/2e38b797329f73a654ba5121691ed76a.png) Wówczas obliczaniu wartości
Wówczas obliczaniu wartości  odpowiada mnożenie
odpowiada mnożenie  a rozwiązywanie układu równań jednorodnych jest w istocie wyznaczaniem miejsc zerowych przekształcenia liniowego
a rozwiązywanie układu równań jednorodnych jest w istocie wyznaczaniem miejsc zerowych przekształcenia liniowego  Przedstawione w poprzedniej sekcji rozumowanie jest przypadkiem szczególnym ogólnego wyniku – zbiór miejsc zerowych przekształcenia liniowego, nazywany jego jądrem, tworzy podprzestrzeń liniową w dziedzinie tego przekształcenia. Wymiar powłoki wspomniany w poprzednim akapicie w przypadku macierzy nazywa się jej rzędem (wierszowym). W ten sposób układ równań liniowych
Przedstawione w poprzedniej sekcji rozumowanie jest przypadkiem szczególnym ogólnego wyniku – zbiór miejsc zerowych przekształcenia liniowego, nazywany jego jądrem, tworzy podprzestrzeń liniową w dziedzinie tego przekształcenia. Wymiar powłoki wspomniany w poprzednim akapicie w przypadku macierzy nazywa się jej rzędem (wierszowym). W ten sposób układ równań liniowych  można traktować jako problem opisu przekształcenia liniowego
można traktować jako problem opisu przekształcenia liniowego  przy czym istnienie rozwiązań jest tożsame z należeniem
przy czym istnienie rozwiązań jest tożsame z należeniem  do obrazu
do obrazu  (czyli istnieniem takiego wektora
(czyli istnieniem takiego wektora  który spełniałby
który spełniałby  ), a ich jednoznaczność jest równoważna trywialności jądra
), a ich jednoznaczność jest równoważna trywialności jądra  (czyli różnowartościowości przekształcenia). Zależność między wymiarami jądra i obrazu opisuje tzw. twierdzenie o rzędzie przekształcenia liniowego.
(czyli różnowartościowości przekształcenia). Zależność między wymiarami jądra i obrazu opisuje tzw. twierdzenie o rzędzie przekształcenia liniowego.
Powyższe obserwacje dotyczące przestrzeni i przekształceń liniowych dla układów jednorodnych zachodzą mutatis mutandis dla przestrzeni i przekształceń afinicznych w przypadku niejednorodnym. W szczególności dowolne rozwiązanie układu niejednorodnego jest translacją rozwiązania odpowiadającego mu układu jednorodnego. Ponadto przekształceniu afinicznemu  przestrzeni
przestrzeni  -wymiarowej w przestrzeń
-wymiarowej w przestrzeń 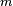 -wymiarową odpowiada przekształcenie liniowe
-wymiarową odpowiada przekształcenie liniowe
 przestrzeni
przestrzeni  -wymiarowej w przestrzeń
-wymiarowej w przestrzeń 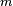 -wymiarową odpowiada przekształcenie liniowe
-wymiarową odpowiada przekształcenie liniowe
przestrzeni  -wymiarowej w przestrzeń
-wymiarowej w przestrzeń  -wymiarową (każda przestrzeń afiniczna może być zanurzona w przestrzeni liniowej wyższego wymiaru). Ostatni wiersz macierzy można pominąć bez utraty ogólności, co tłumaczy obserwację poczynioną w sekcji postać i zapis.
-wymiarową (każda przestrzeń afiniczna może być zanurzona w przestrzeni liniowej wyższego wymiaru). Ostatni wiersz macierzy można pominąć bez utraty ogólności, co tłumaczy obserwację poczynioną w sekcji postać i zapis.
 -wymiarowej w przestrzeń
-wymiarowej w przestrzeń  -wymiarową (każda przestrzeń afiniczna może być zanurzona w przestrzeni liniowej wyższego wymiaru). Ostatni wiersz macierzy można pominąć bez utraty ogólności, co tłumaczy obserwację poczynioną w sekcji postać i zapis.
-wymiarową (każda przestrzeń afiniczna może być zanurzona w przestrzeni liniowej wyższego wymiaru). Ostatni wiersz macierzy można pominąć bez utraty ogólności, co tłumaczy obserwację poczynioną w sekcji postać i zapis.
 oraz
oraz  jest
jest  i jej następnika za
i jej następnika za  da dwie tożsamości.
da dwie tożsamości.





![[x_1 a_{11} + \dots + x_n a_{1n},\ \dots,\ x_1 a_{m1} + \dots + x_n a_{mn}] = [b_1, \dots, b_m],](http://upload.wikimedia.org/math/5/e/7/5e7490b8027cef4dbaff40c6c69516bd.png)
![x_1[a_{11}, \dots, a_{m1}] + \dots + x_n[a_{1n}, \dots, a_{mn}] = [b_1, \dots, b_m],](http://upload.wikimedia.org/math/a/f/a/afa627bae048c9494793afae34dde25f.png)





![\left[\begin{matrix} a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} & \dots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \dots & a_{mn} \end{matrix}\right|\left.\begin{matrix} b_1 \\ b_2 \\ \vdots \\ b_m \end{matrix}\right].](http://upload.wikimedia.org/math/7/8/4/784204e5c9c496d52a2f41829eef5c2f.png)




 oraz
oraz  tworzą układ sprzecznyRozwiązaniem
tworzą układ sprzecznyRozwiązaniem

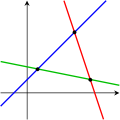

 oraz
oraz  nie są liniowo niezależne.
nie są liniowo niezależne.






Brak komentarzy:
Prześlij komentarz